Определение ставки дисконта при оценке инвестиций

Валерий Солодов
старший консультант МАГ КОНСАЛТИНГ

Введение

В настоящей статье мы проанализируем некоторые практические аспекты применения методов оценки эффективности инвестиций (см. "ФГ" № 15, 2004), с которыми пришлось столкнуться в ходе выполнения консультационных проектов. Однако следует отметить, что их можно рассматривать лишь как частные вопросы, но не как выявленные общие закономерности, присущие любым отраслям и рынкам.

Как известно, российские рынки в экономическом смысле явно являются несовершенными (т.е., например, если рынок так или иначе монополизирован или олигополизирован, то это отражается на полноте и доступности информации о товарах и услугах и, как следствие, на ценах). В связи с этим многие разработанные на Западе подходы, будучи методологически верными, при их реальном применении у нас наталкиваются на значительные трудности, связанные с получением достоверных статистических данных по отрасли, большими различиями в ценах на источники финансирования и нормах приемлемости, отсутствием институтов рейтингования и др.

Все известные методы оценки эффективности инвестиционных проектов относятся к проектам, которые рассматриваются не только до начала их реализации, но и еще до принятия их в качестве направления вложения средств. Между тем представляет интерес также и вопрос назначения соответствующих ставок, норм и критериев в ходе выполнения (реализации) инвестиционного проекта.

Факторы, влияющие на ставку дисконта

На этапе оценки проекта на выбор ставки дисконта влияют такие факторы, как:

• инфляция;
• уровень доходности;
• ставка ссудного процента (если берется ссуда);
• ставка рефинансирования;
• рентабельность активов (ROA) или собственного капитала (ROE);
• доходность на инвестиции портфеля;
• риски.

Что касается первого и последнего факторов, то ввиду особого экономического смысла их влияние мы предлагали учитывать отдельно, после всех расчетов по оценке предполагаемых инвестиций (в программном продукте Project Expert, считающемся почти официально признанным и рекомендованным для использования инвесторами в странах СНГ, дисконтирование проводится автономно от инфляции, т.е. ставку дисконта и уровень инфляции аналитик задает независимо одну от другой). Приведенным списком эти факторы могут не ограничиваться, помимо указанных в конкретных условиях могут действовать и другие.

При рассмотрении существующих методик оценки эффективности инвестиционных проектов методологически неясно, каким образом такие разные по экономическому смыслу величины, как инфляция, риски, доходность на инвестиции портфеля, можно объединить в одном показателе г - ставка дисконта. Смысл такого показателя становится неопределенным, частные влияния параметров, входящих в него, в модели не отражены. Во всяком случае, если бы даже был принят такой подход, нужна была бы особая процедура для определения ставки дисконта. Однако видно, что какая-либо специальная модель отсутствует, за исключением нескольких, таких как модель Гордона, САРМ и опционная модель оценки доходности.

Во всех приведенных моделях, за исключением САРМ, их экономическое и математическое обоснование применения для оценки уровня ставки дисконта отсутствует. Заложенная в САРМ концепция пригодна лишь для типичных случаев.

Определение рисков

Не ставя задачу полностью описать все подходы риск-менеджмента, превратившегося в последнее время в отдельную дисциплину, приведем лишь некоторые мало известные инструменты, которые могут способствовать более адекватному определению рисков, присущих инвестиционному проекту. Как было сказано ранее, наиболее адекватным определением денежного потока была бы мнемоническая формула:

"Денежный поток = деньги получаемые < чистой прибыли + деньги вероятные < чистой прибыли х вероятность их получения".

Как в случае оценки эффективности предполагаемых инвестиций, так и в случае инвестиционного учета, т.е. оценки эффективности сделанных инвестиций, без начислений часто не обойтись. Последние же всегда связаны с вероятностным характером предполагаемых доходов (дебиторская задолженность) или расходов (кредиторская). При этом различные активы могут иметь разные характеристики, связанные с рисками. Даже в структуре одного актива (например, дебиторской задолженности) различные составляющие могут иметь разные распределения вероятностей:

• если покупатели продукции предприятия относятся к разным (некоррелированным) отраслям, то спад в одной отрасли и платежеспособность данного покупателя могут быть никак не связаны с отраслью и платежеспособностью другого покупателя;
• если потребители принадлежат к одной и той же или к коррелированным отраслям, то расчет ввиду наличия статистической связи усложняется, за исключением того случая, когда можно сделать статистически корректное предположение об идентичных вероятностных характеристиках дебиторской задолженности данных потребителей;
• другие активы (а также пассивы) также могут быть распределенными величинами, например основные средства или нематериальные активы, оцениваемые на какой-либо будущий момент хода реализации инвестиционного проекта по рыночной стоимости.

Говоря о рисках, необходимо иметь в виду еще одну проблему - понимание риска в настоящее время неоднозначно. Чаще всего его представляют как:

• риск-вероятность;
• риск-отклонение;
• различные свертки первых двух величин.

Теория финансовых рисков базируется на понятии метрического пространства "риск-доходность" нобелевского лауреата Гарри Марковица, где указанные параметры являются двумя измерениями данного пространства, точка или область в котором определяет состояние соответствующего актива или инвестиционного портфеля. При этом данная теория основывается на понимании риска как среднеквадратичного отклонения (СКО), что предполагает симметричность вероятностных распределений. Однако, например, при оценке риска портфеля, в котором есть опционы, теория портфеля Г. Марковица неприменима, так как вероятностное распределение несимметрично. Вообще, там, где распределения несимметричны, понимание риска как отклонения (СКО, дисперсия или вариация) некорректно. Хеджирование в той или иной степени основано на искажении распределения в пользу хеджера. Это обстоятельство заставляет осторожно подходить к применению данного подхода в разных случаях.

Полезность (по Сэвиджу и др.)

Любые показатели риска сами по себе еще не дают полной картины последствий того или иного сценария, который произойдет в будущем, для экономического состояния бизнес-субъекта. Например, выход NPV в область отрицательных значений с какой-либо вероятностью Р = Р (NPV < 0) может нести по-разному оцениваемые субъективные последствия для инвестора, вынужденного вкладывать все свои средства в один большой проект, и для венчурного инвестора, который диверсифицирует свои вложения. Для первого субъективный ущерб от убытков (финансовый крах, катастрофа) будет гораздо выше, чем для второго (одно из вложений неудачное). Для учета таких факторов в экономике существует теория полезности, основанная на понятии предельной полезности. Рассмотрим применение величины полезности в теории рисков.

Допустим, что некоторому множеству исходов - событий X_i  сопоставлены их вероятности P_i. Распределение этих вероятностей может быть разным в зависимости от решения с номерами /, 2, ... в индексах P_i. Каждому исходу присваиваются численные значения функции U_i , называемой функцией полезности (см. таблицу). Эта функция может выражать в числах некую экономическую полезность данного исхода.

Решение "1" даст ожидаемую полезность: 0,6 х 6+0,0 х 5+0,0 х 4+0,4 х 3 = 3,6+0+0+1,2 = 4,8, решение "2": 0,0 х 6+0,6 х 5 + 0,4 х 4+0,0 хЗ = 0+3,0+1,6+0=4,6, то есть будет принято 1-е решение. Та же функция U может придавать событиям с равными вероятностями разные величины полезности и т.д.

Еще меньшее внимание уделяется правилам-рекомендациям по принятию решений в условиях полной неопределенности: правилу Вальда, правилу Сэвиджа и правилу Гурвица. По самому названию ("принятие решений") речь идет, по сути, об управлении, поэтому этот подход называют иногда "управленческим".

Пример определения ставки дисконта

Рассмотрим практический пример. Для крупной организации необходимо было разработать модель как оценки эффективности предполагаемых инвестиционных проектов, так и оценки эффективности проектов, которые уже реализуются.

При определении ставки дисконта выяснилось, что:

• статистические данные по инвестиционному учету в компании с обратным временным горизонтом более года практически отсутствуют;
• данные бухгалтерского учета, из которых можно было бы восстановить картину осуществленных инвестиций и их возмещений, мало пригодны для данных целей;
• рынок, на котором ведет свою деятельность компания, закрытый, т.е. получение информации затруднено и данные недостоверны;
• основная организационно-правовая форма деятельности - закрытое акционерное общество;
• дивидендная политика отсутствует;
• ранее таких целей, как учет инвестиций, не ставилось, поэтому все сведения о деятельности, которые выходили бы за рамки финансового учета, найти невозможно.

Данную ситуацию можно считать достаточно типичной для многих предприятий и отраслей.

В расчете NPV ставку дисконтирования необходимо определять особо. Для конкретного предприятия при неразвитых фондовых рынках можно предложить следующие методы ее оценки:

метод 1. С учетом таких показателей, как достигнутая в прошлых периодах годовая ставка доходности компании, ставка рефинансирования Центрального банка Российской Федерации, прогнозы доходности компании и отрасли на предстоящий период, данные по сравниваемым компаниям данной отрасли, доходность инструментов рынка (или просто инвестиций в компании данной отрасли), определяется базовая ставка дисконта;

метод 2. На основе экспертных оценок, то есть когда ставка устанавливается как результирующая величина исходя из мнений нескольких экспертов в данной области;

метод 3. Определяется как средневзвешенная величина:

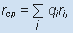
где r_cp - какая-либо оцениваемая величина;
r_i - частная оценка оцениваемой величины;
q_i - вес, придаваемый данной оценке r_i (относительная значимость данной частной оценки по сравнению с другими, выраженная числовым значением), сумма этих весов равна 1.

Удобным способом назначения этих весов может быть следующая процедура:

1) выбирается наименьший вес и принимается равным единице;
2) по сравнению с ним, а также по сравнению друг с другом выбираются другие веса (то есть главное - выбрать взаимные соотношения весов);
3) суммируются все полученные веса;
4) полученная сумма берется в степени "минус 1" (то есть единица делится на полученную сумму);
5) принятые веса умножаются на полученное в п. 4 число.