Дисконтированное движение денежных средств (DCF)
Учебный курс АССА
Цели
После изучения этого блока Вы сможете:
- объяснить, что такое стоимость денег с учетом фактора времени;
- использовать метод чистой текущей стоимости (NPV);
- использовать метод оценки внутреннего уровня доходности (IRR);
- сравнивать и противопоставлять NPV и IRR методы.
Оценка программ капиталовложений
Важным инструментом в аналитическом наборе финансового директора является дисконтированное движение денежных средств (DCF). Оно используется в первую очередь при оценке инвестиционных программ, которые мы будем рассматривать подробно в блоке 38. В этом блоке мы рассмотрим основы метода DCF.
Инвестиционная программа - это проект, который приносит прибыль на протяжении ряда периодов. Следовательно, он включает потоки дохода на протяжении будущих периодов. Оценка таких проектов обычно основывается на оценке потоков денежных средств, которые они вызывают. Процесс оценки призван не только оценить отдельные проекты, но также определить, какой из ряда проектов является лучшим.
Задание
Вы консультируете компанию, которая решает, какой из двух проектов реализовать. Ваша первая задача будет состоять в том, чтобы определить потоки денежных средств, возникающие из них. Потоки денежных средств показаны ниже. Какой же проект лучше?
| Год | Проект А | Проект В | |
| $ | $ | ||
| Первоначальные затраты | 0 | (2,000) | (2,000) |
| Чистый приток денежных средств | 1 | 1,000 | 300 |
| Чистый приток денежных средств | 2 | 1,000 | 500 |
| Чистый приток денежных средств | 3 | 500 | 1,800 |
| Суммарный приток денежных средств | 2,500 | 2,600 | |
| Остаточный поток денежных средств | 500 | 600 |
На основе простого потока средств Вы могли бы подумать, что программа В более привлекательна, чем программа А, потому что ее остаточный поток денежных средств больше. Но у этих потоков денежных средств есть один важный аспект, а именно: их распределение по времени. Денежные средства, полученные через три года, сравниваются здесь на эквивалентной основе с деньгами, выплачиваемыми в данный момент (год 0) и деньгами, получаемыми в 1-й и 2-й годы. Из опыта мы знаем, что $1, полученный сейчас, имеет большую стоимость, чем $1, полученный через три года. Деньги действительно имеют "временной фактор стоимости", и инфляция не единственная причина этого. Даже в условиях нулевой инфляции $1, полученный в данный момент, ценнее, чем $1, полученный через три года. Это связано с тем, что деньги имеют "инвестиционную стоимость". Если $1, полученный сегодня, инвестируется, скажем, под 10%, то он будет стоить:
| $1.1 | через 1 год | ($1 + 10%) | = ($1 + 10%) |
| $1.21 | через 2 года | ($1.1 + 10%) | = ($1 + 10%)2 |
| $1.33 | через 3 года | ($1.21 + 10%) | = ($1 + 10%)3 |
В обратной последовательности это означает, что получение $1.33 через три года эквивалентно получению $1 сегодня. Точно так же, если $1 будет получен в будущем, то его эквивалент сегодня равняется:
Полученный через 1 год = $0.909 сегодня или (1/1.1)
Полученный через 2 года = $0.826 сегодня или (1/1.21)
Полученный через 3 года = $0.751 сегодня или (1/1.33)
Путем применения этих корректировок к будущим поступлениям они конвертируются в фунты текущей стоимости и непосредственно сопоставимы друг с другом. Эта общепринятая мера называется "текущей стоимостью". Таблицы, показывающие значения текущей стоимости по годам и процентным ставкам, являются общедоступными (см. таблицы 37.9 и 37.10).
Чистая текущая стоимость
Если мы допустим, что деньги могут быть инвестированы под 12% годовых, и применим коэффициенты текущей стоимости, соответствующие 12% (см. таблицу 37.9) к оценке проектов А и В из предыдущего задания, мы получим показатели, представленные в таблице 37.1.
| Год | Чистый поток денежных средств | Коэффи- циент дисконти- рования 12% | Текущая стоимость | |||
| Проект | А | В | А | В | ||
| Первоначальные затраты | 0 | (2,000) | (2,000) | 1.000 | (2,000) | (2,000) |
| Чистый приток денежных средств | 1 | 1,000 | 300 | 0.893 | 893 | 268 |
| Чистый приток денежных средств | 2 | 1,000 | 500 | 0.797 | 797 | 398 |
| Чистый приток денежных средств | 3 | 500 | 1,800 | 0.712 | 356 | 1,281 |
| Суммарный приток денежных средств | 2,500 | 2,600 | 2,046 | 1,947 | ||
| Остаточный поток денежных средств | 500 | 600 | ||||
| Чистая текущая стоимость | 46 | (53) | ||||
Таблица 37.1
После того как рассчитаны и суммированы значения текущей стоимости, текущая стоимость исходного капиталовложения вычитается из суммарного притока денежных средств, что дает чистую текущую стоимость. (Обратите внимание на то, что текущая стоимость исходного капиталовложения всегда будет такой же, как и само капиталовложение, потому что $1, истраченный сейчас, имеет текущую стоимость $1).
Вы видите, что когда все будущие потоки денежных средств переводятся в текущую стоимость, проект А оказывается более привлекательным, чем проект В. А это противоположно оценке на основе простого потока денежных средств. Расчет чистой текущей стоимости дает более значимый результат. Чистая текущая стоимость $46 означает, что проект А дает прибыль $46 в оценке настоящего времени, что гораздо больше, чем мы получили бы, инвестировав оставшиеся средства (первоначальная инвестиция минус поступающие потоки денежных средств) под 12% годовых. Отрицательное значение чистой текущей стоимости $53 в проекте В указывает на то, что он не только не так привлекателен, как проект А, но и что инвестирование остающихся средств под 12% годовых принесло бы прибыль на $53 больше, в $ текущей стоимости. Поступающие потоки денежных средств в проекте В недостаточны для того, чтобы обеспечить обслуживание средств на уровне 12% годовых и возместить предоставленные средства в течение и к концу срока осуществления проекта.
Метод оценки стоимости дисконтированных потоков денежных средств (DCF)
Это альтернативный метод оценки стоимости потоков денежных средств, использующий метод DCF. Иногда его называют методом внутреннего уровня доходности (IRR).
Метод NPV определял проект, который был наиболее привлекательным по DCF, но он не давал внутреннего уровня доходности в любом случае. Метод стоимости DCF или IRR рассчитывает внутренний уровень доходности по каждому проекту. Эти результаты можно сравнить с требуемой прибылью или имеющимися прибылями от других проектов, чтобы определить, какой проект следует осуществлять,
Стоимость DCF - это ставка дисконта, которая будет уравнивать текущую стоимость суммарных исходящих потоков денежных средств в проекте с текущей стоимостью суммарных поступающих потоков денежных средств. Это даст нулевую NPV.
Задание
Попробуйте рассчитать методом проб и ошибок стоимость DCF, такую ставку, которая даст нулевое значение NPV для проекта А, приведенного выше. (Подсказка: попробуйте ставку дисконта 14%.)
При 12% проект А имеет положительную NPV, $46. Это означает, что ставка дисконта должна быть выше, чем 12% для получения соответствующей прибыли от проекта. Но $46 - небольшая сумма относительно средств, связанных в проекте на протяжении срока его реализации, так что эта ставка не должна быть значительно выше 12%.
Таблица 37.2 показывает ставку дисконта, равную 14%. Оказывается, что эквивалентная сумма средств, инвестированная под 14% годовых, принесла бы более высокую прибыль, чем проект, поэтому фактическая прибыль должна быть меньше 14 %.
| Проект А: | Год | Чистый денежный поток | 14%-й коэффи- циент дисконта | NPV | 12%-й коэффи- циент дисконта | NPV |
| Первоначальные затраты | 0 | (2,000) | 1,000 | (2,000) | 1,000 | (2,000) |
| Чистый приток средств | 1 | 1,000 | 0.877 | 877 | 0.893 | 893 |
| Чистый приток средств | 2 | 1,000 | 0.769 | 769 | 0.797 | 797 |
| Чистый приток средств | 3 | 500 | 0.675 | 337 | 0.712 | 356 |
| Суммарный приток средств | 2,500 | 1,983 | 2,046 | |||
| Остаточный поток средств | (500) | |||||
| Чистая текущая стоимость | (17) | 46 |
Таблица 37.2
Норма прибыли по проекту А находится где-то между 12% и 14%. С помощью интерполяции мы теперь можем найти фактическую норму прибыли:
| Ставка дисконта | Текущая стоимость |
| 12% | 46 |
| 14% | (17) |
| 2% | 63 |
Путем увеличения внутреннего уровня доходности с 12% до 14% NPV была сокращена на $63. Однако ее необходимо уменьшить лишь на $46, следовательно процентная ставка должна быть увеличена на:
| 46 | |
| ------ | х 2 = 1.46% |
| 63 |
и 12% + 1.46% = 13.46%
Таким образом норма прибыли DCF по проекту равняется 13.46%. Это означает, что прибыль от средств, связанных в проекте на протяжении всего срока его осуществления, дала бы такую же норму прибыли, как если бы они были инвестированы под 13.46% годовых. Это иллюстрирует таблица 37.3. Важно обратить внимание на то, что годовую прибыль предполагается реинвестировать и включить в средства, инвестируемые на следующий год.
| Проект А Год | Инвестированные средства | Проценты при 13.46% | Накапливаемый остаток | Приток денежных средств | Конечный остаток |
| 1 | 2,000 | 270 | 2,270 | 1,000 | 1,270 |
| 2 | 1,270 | 171 | 1,441 | 1,000 | 441 |
| 3 | 441 | 59 | 500 | 500 | ноль |
| 500 | 2,500 |
Таблица 37.3
Из таблицы 37.3 мы видим, что проектируемые притоки денежных средств обеспечивают достаточные суммы для того, чтобы возместить все инвестированные средства и проценты, причитающиеся при 13.46%, если бы это была желаемая или требуемая ставка.
IRR можно также найти путем построения графика, называемого графиком текущей стоимости. Если на графике изображены положительная и отрицательная NPV, соединенные между собой прямой линией, то точка, в которой линия пересекает линию ставки дисконта, может быть принята за приблизительное значение IRR. Для значений, рассчитанных выше, это показано на рисунке 37.1.
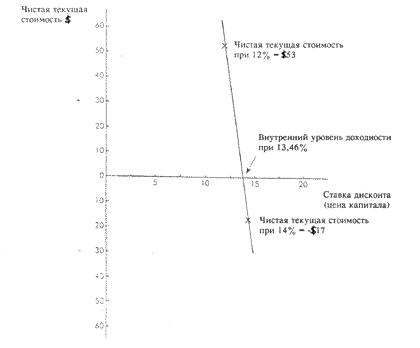
Рисунок 37.1 График текущей стоимости
Сравнение методов NPV и IRR
Как правило, оба эти метода приводят к одинаковым решениям на "принятие" или "отклонение". Но есть обстоятельства, в которых они могут дать противоположные результаты:
- когда проекты имеют противоположные фазы потока денежных средств;
- когда проекты имеют разные по размерам затраты;
- когда проекты различаются по продолжительности во времени;
- когда имеются нерегулярные потоки денежных средств, вызывающие на протяжении периода реализации проекта череду доходов и расходов, приводящие к многочисленным IRR.
Чтобы проиллюстрировать это, мы снова рассмотрим проекты А и В, но изменим поток денежных средств для проекта В. Теперь они выглядят так, как показано в таблице 37.4.
| Год | Проект А | Проект В | |
| Первоначальные затраты | 0 | (2,000) | (2,000) |
| Чистый приток денежных средств | 1 | 1,000 | 800 |
| Чистый приток денежных средств | 2 | 1,000 | 0 |
| Чистый приток денежных средств | 3 | 500 | 1,870 |
| Суммарный приток денежных средств | 2,500 | 2,670 | |
| Остаточный поток денежных средств | 500 | 670 | |
| Внутренний уровень доходности | 13.5% | 13.1% |
Таблица 37.4
Теперь Проект А лишь незначительно привлекательнее, чем проект В. Это связано с тем, что больше средств денежного потока возникает на более раннем этапе реализации проекта, и предполагается, что прибыли реинвестируются с IRR. Однако это не всегда может быть так, поскольку возможности инвестировать эти средства с таким уровнем доходности могут отсутствовать.
Задание
Допуская, что ставка дисконта будет равняться требуемой норме прибыли, какой проект Вы бы выбрали при 12%? Рассчитайте текущую стоимость для обоих проектов при 12%.
Таблица 37.5 показывает предпосылки изменений распределения во времени потоков денежных средств для ставки дисконта 12%. Конечно же показатели для проекта А остаются такими же, как и раньше (рисунок 37.1), поскольку его поток денежных средств не изменился. (Коэффициенты берутся из таблицы 37.9).
| Год | Чистый поток денежных средств | Коэффи- циент дисконти- рования 12% | Текущая стоимость | |||
| Проект | А | В | А | В | ||
| Первоначальные затраты | 0 | (2,000) | (2,000) | 1.000 | (2,000) | (2,000) |
| Чистый приток денежных средств | 1 | 1,000 | 800 | 0.893 | 893 | 714 |
| Чистый приток денежных средств | 2 | 1,000 | 0 | 0.797 | 797 | 0 |
| Чистый приток денежных средств | 500 | 1,870 | 0.712 | 356 | 1,332 | |
| Суммарный чистый поток денежных средств | 500 | 670 | ||||
| Чистая текущая стоимость | 46 | 46 | ||||
Таблица 37.5
Здесь возникает дилемма, потому что NPV абсолютно одинакова в обоих случаях. В идеальном мире определенности вам безразлично, какой проект выбирать, А или В, потому что NPV одинакова. Так какой же следует выбрать? Проект А имеет более высокий уровень доходности IRR, и по этой причине выбрать следует его. Это может оказаться правильным, но было бы неверно допускать, что проект с наивысшей IRR обязательно следует выбирать. В таблице 37.6 вновь рассматриваются проекты А и В при ставке дисконта 10%.
| Год | Чистый поток денежных средств | Коэффи- циент дисконти- рования 12% | Текущая стоимость | |||
| Проект | А | В | А | В | ||
| Первоначальные затраты | 0 | (2,000) | (2,000) | 1.000 | (2,000) | (2,000) |
| Чистый приток денежных средств | 1 | 1,000 | 800 | 0.909 | 909 | 727 |
| Чистый приток денежных средств | 2 | 1,000 | 0 | 0.826 | 826 | 0 |
| Чистый приток денежных средств | 500 | 1,870 | 0.751 | 375 | 1,404 | |
| Суммарный чистый поток денежных средств | 500 | 670 | ||||
| Чистая текущая стоимость | 110 | 131 | ||||
Таблица 37.6
Это создает дополнительную проблему, потому что проект В теперь показывает более высокую NPV, чем проект А. Возникает прямое противоречие между выбором, предложенным по методу NPV, проект В, и выбором, предложенным по методу IRR, проект А.
Схема, показанная в таблице 37.7, обобщает NPV проектов А и В для диапазона ставок дисконта и варианты выбора, на которые указывают методы NPV и IRR.
| NPV | Предпочти- тельный вариант | IRR | Предпочти- тельный вариант | |||
| Ставка дисконта | А | В | А | В | ||
| 6% | 253 | 325 | В | 13.5 | 13.1 | А |
| 8% | 180 | 226 | В | 13.5 | 13.1 | А |
| 10% | 110 | 131 | В | 13.5 | 13.1 | А |
| 12% | 46 | 46 | Любой | 13.5 | 13.1 | А |
| 13% | 15 | 4 | А | 13.5 | 13.1 | А |
| 14% | (16) | (36) | А | 13.5 | 13.1 | А |
| 16% | (75) | (113) | А | 13.5 | 13.1 | А |
Таблица 37.7
Их также можно представить графически, как показано на Рисунке 37.2.
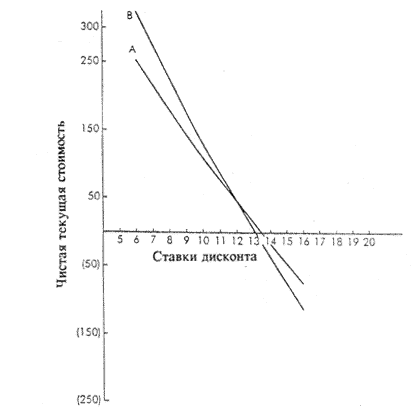
Рисунок 37.2 Чистая текущая стоимость в диапазоне ставок дисконта
Значения NPV располагаются по вертикальной оси, а ставки дисконта - по горизонтальной. Две линии А и В пересекаются на значении ставки дисконта в 12% и NPV - 46, и каждая пересекает горизонтальную ось в точке, соответствующей ее значению IRR, т.е. 13.5 для А и 13.1 для В. По методу NPV, когда ставка дисконта падает ниже 12%, проект В становится более привлекательным. Когда она превышает 12%, более привлекательным оказывается А.
Какой же метод лучше?
Так как в метод IRR заложено допущение реинвестирования, метод NPV считается самым подходящим. Отдать ему предпочтение также заставляет факт, что IRR не учитывает уровень инвестиции и, таким образом, абсолютный уровень прибыли на нее. К примеру, он может показать хорошую прибыль на небольшую инвестицию в сравнении с меньшей прибылью на значительно большую инвестицию. В таких случаях практическое предпочтение будет отдаваться большей инвестиции, и это также будет показываться в расчетах NPV.
Приростные потоки денежных средств
Если необходимо составить окончательное мнение относительно того, какой вариант правильно было бы выбрать, то это можно сделать, применив метод нормы DCF к приростным потокам денежных средств между двумя проектами. Давайте посмотрим на приростные потоки денежных средств, возникающие в результате решения о принятии проекта В, при ставке дисконта 12%, несмотря на то, что проект А имеет более высокое значение IRR (см. таблицу 37.8). Норма прибыли DCF при этом приблизительно равняется 12% и поскольку это соответствует потребной норме 12%, любой проект следовало бы принять.
| Чистые денежные средства | Коэффи- циент дисконти- рования | ||||
| Год | А | В | В - А | 12% | NPV |
| 0 | (2,000) | (2,000) | 0 | 1.000 | 0 |
| 1 | 1,000 | 800 | (200) | 0.893 | 179 |
| 2 | 1,000 | 0 | (1,000) | 0.797 | 797 |
| 3 | 500 | 1,870 | 1,370 | 0.712 | (975) |
| Чистый поток средств | 500 | 670 | (170) | ||
| NPV | (1) | ||||
Таблица 37.8
Использование анализа приростных потоков денежных средств убеждает воспользоваться NPV вместо IRR в случаях возникновения спорных ситуаций. Метод NPV концептуально верен и требует только одного блока вычислений. IRR менее надежен, чем NPV. Но поскольку процентные показатели прибыли все еще широко используются управлением для измерения и контроля, IRR удобен, с точки зрения оценки прибыли для сравнительных целей, при условии, что управление знает о неожиданностях.
Контрольное задание
Управление компании С Ко плк предполагает вложить $25,000 в проект с потенциальным сроком существования 6 лет. Цена капитала компании составляет 18% в год. Проект может быть прекращен в конце любого года, а оборудование и запас проданы. Чистый поток денежных средств и значения (остаточной) стоимости при отказе прогнозируются следующим образом:
| Год | Чистые потоки денежных средств | Стоимость при отказе |
| $ | $ | |
| 0 | (25,000) | |
| 1 | 4,000 | 22,500 |
| 2 | 6,000 | 18,000 |
| 3 | 10,000 | 16,000 |
| 4 | 10,000 | 15,000 |
| 5 | 10,000 | 12,500 |
| 6 | 10,000 | 0 |
Проконсультируйте управление компании.
Налоги не учитывайте.
Таблица 37.9 Текущая стоимость 1 при сложном проценте:
(1 + r)-n
| Годы (n) | Процентные ставки (r) | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0.9901 | 0.9804 | 0.9709 | 0.9615 | 0.9524 | 0.9434 | 0.9346 | 0.9259 | 0.9174 | 0.9091 |
| 2 | 0.9803 | 0.9612 | 0.9426 | 0.9246 | 0.9070 | 0.8900 | 0.8734 | 0.8573 | 0.8417 | 0.8264 |
| 3 | 0.9706 | 0.9423 | 0.9151 | 0.8890 | 0.8638 | 0.8396 | 0.8163 | 0.7938 | 0.7722 | 0.7513 |
| 4 | 0.9610 | 0.9238 | 0.8885 | 0.8548 | 0.8227 | 0.7921 | 0.7629 | 0.7350 | 0.7084 | 0.6830 |
| 5 | 0.9515 | 0.9057 | 0.8626 | 0.8219 | 0.7835 | 0.7473 | 0.7130 | 0.6806 | 0.6499 | 0.6209 |
| 6 | 0.9420 | 0.8880 | 0.8375 | 0.7903 | 0.7462 | 0.7050 | 0.6663 | 0.6302 | 0.5963 | 0.5645 |
| 7 | 0.9327 | 0.8706 | 0.8131 | 0.7599 | 0.7107 | 0.6651 | 0.6227 | 0.5835 | 0.5470 | 0.5132 |
| 8 | 0.9235 | 0.8535 | 0.7894 | 0.7307 | 0.6768 | 0.6274 | 0.5820 | 0.5403 | 0.5019 | 0.4665 |
| 9 | 0.9143 | 0.8368 | 0.7664 | 0.7026 | 0.6446 | 0.5919 | 0.5439 | 0.5002 | 0.4604 | 0.4241 |
| 10 | 0.9053 | 0.8203 | 0.7441 | 0.6756 | 0.6139 | 0.5584 | 0.5083 | 0.4632 | 0.4224 | 0.3855 |
| 11 | 0.8963 | 0.8043 | 0.7224 | 0.6436 | 0.5847 | 0.5268 | 0.4751 | 0.4289 | 0.3875 | 0.3505 |
| 12 | 0.8874 | 0.7885 | 0.7014 | 0.6246 | 0.5568 | 0.4970 | 0.4440 | 0.3971 | 0.3555 | 0.3186 |
| 13 | 0.8787 | 0.7730 | 0.6810 | 0.6006 | 0.5303 | 0.4688 | 0.4150 | 0.3677 | 0.3262 | 0.2897 |
| 14 | 0.8700 | 0.7579 | 0.6611 | 0.5775 | 0.5051 | 0.4423 | 0.3878 | 0.3405 | 0.2992 | 0.2633 |
| 15 | 0.8613 | 0.7430 | 0.6419 | 0.5553 | 0.4810 | 0.4173 | 0.3624 | 0.3152 | 0.2745 | 0.2394 |
| 16 | 0.8528 | 0.7284 | 0.6232 | 0.5339 | 0.4581 | 0.3936 | 0.3387 | 0.2919 | 0.2519 | 0.2176 |
| 17 | 0.8444 | 0.7142 | 0.6050 | 0.5134 | 0.4363 | 0.3714 | 0.3166 | 0.2703 | 0.2311 | 0.1978 |
| 18 | 0.8360 | 0.7002 | 0.5874 | 0.4936 | 0.4155 | 0.3503 | 0.2959 | 0.2502 | 0.2120 | 0.1799 |
| 19 | 0.8277 | 0.6864 | 0.5703 | 0.4746 | 0.3957 | 0.3305 | 0.2765 | 0.2317 | 0.1945 | 0.1635 |
| 20 | 0.8195 | 0.6730 | 0.5537 | 0.4564 | 0.3769 | 0.3118 | 0.2584 | 0.2145 | 0.1784 | 0.1486 |
| 25 | 0.7795 | 0.6095 | 0.4776 | 0.3751 | 0.2953 | 0.2330 | 0.1842 | 0.1460 | 0.1160 | 0.0923 |
| 30 | 0.7419 | 0.5521 | 0.4120 | 0.3083 | 0.2314 | 0.1741 | 0.1314 | 0.0994 | 0.0754 | 0.0573 |
| 35 | 0.7059 | 0.5000 | 0.3554 | 0.2534 | 0.1813 | 0.1301 | 0.0937 | 0.0676 | 0.0490 | 0.0356 |
| 40 | 0.6717 | 0.4529 | 0.3066 | 0.2083 | 0.1420 | 0.0972 | 0.0668 | 0.0460 | 0.0318 | 0.0221 |
| 45 | 0.6391 | 0.4102 | 0.2644 | 0.1712 | 0.1113 | 0.0727 | 0.0476 | 0.0313 | 0.0207 | 0.0137 |
| 50 | 0.6080 | 0.3715 | 0.2281 | 0.1407 | 0.0872 | 0.0543 | 0.0339 | 0.0213 | 0.0134 | 0.0085 |
| Годы (n) | Процентные ставки (r) | |||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 1 | 0.9009 | 0.8929 | 0.8850 | 0.8772 | 0.8696 | 0.8621 | 0.8547 | 0.8475 | 0.8403 | 0.8333 |
| 2 | 0.8116 | 0.7972 | 0.7831 | 0.7695 | 0.7561 | 0.7432 | 0.7305 | 0.7182 | 0.7062 | 0.6944 |
| 3 | 0.7312 | 0.7118 | 0.6831 | 0.6750 | 0.6575 | 0.6407 | 0.6244 | 0.6086 | 0.5934 | 0.5787 |
| 4 | 0.6587 | 0.6355 | 0.6133 | 0.5921 | 0.5718 | 0.5523 | 0.5337 | 0.5158 | 0.4987 | 0.4823 |
| 5 | 0.5935 | 0.5674 | 0.5428 | 0.5194 | 0.4972 | 0.4761 | 0.4561 | 0.4371 | 0.4190 | 0.4019 |
| 6 | 0.5346 | 0.5066 | 0.4803 | 0.4556 | 0.4323 | 0.4104 | 0.3898 | 0.3704 | 0.3521 | 0.3349 |
| 7 | 0.4817 | 0.4523 | 0.4251 | 0.3996 | 0.3759 | 0.3538 | 0.3332 | 0.3139 | 0.2959 | 0.2791 |
| 8 | 0.4339 | 0.4039 | 0.3762 | 0.3506 | 0.3269 | 0.3050 | 0.2848 | 0.2660 | 0.2487 | 0.2326 |
| 9 | 0.3909 | 0.3606 | 0.3329 | 0.3075 | 0.2843 | 0.2630 | 0.2434 | 0.2255 | 0.2090 | 0.1938 |
| 10 | 0.3522 | 0.3220 | 0.2946 | 0.2697 | 0.2472 | 0.2267 | 0.2080 | 0.1911 | 0.1756 | 0.1615 |
| 11 | 0.3173 | 0.2875 | 0.2607 | 0.2366 | 0.2149 | 0.1954 | 0.1778 | 0.1619 | 0.1476 | 0.1346 |
| 12 | 0.2858 | 0.2567 | 0.2307 | 0.2076 | 0.1869 | 0.1685 | 0.1520 | 0.1372 | 0.1240 | 0.1122 |
| 13 | 0.2575 | 0.2292 | 0.2042 | 0.1821 | 0.1625 | 0.1452 | 0.1299 | 0.1163 | 0.1042 | 0.0935 |
| 14 | 0.2320 | 0.2046 | 0.1807 | 0.1597 | 0.1413 | 0.1252 | 0.1110 | 0.0985 | 0.0876 | 0.0779 |
| 15 | 0.2090 | 0.1827 | 0.1599 | 0.1401 | 0.1229 | 0.1079 | 0.0949 | 0.0835 | 0.0736 | 0.0649 |
| 16 | 0.1883 | 0.1631 | 0.1415 | 0.1229 | 0.1069 | 0.0930 | 0.0811 | 0.0708 | 0.0618 | 0.0541 |
| 17 | 0.1696 | 0.1456 | 0.1252 | 0.1078 | 0.0929 | 0.0802 | 0.0693 | 0.0600 | 0.0520 | 0.0451 |
| 18 | 0.1528 | 0.1300 | 0.1108 | 0.0946 | 0.0808 | 0.0691 | 0.0592 | 0.0508 | 0.0437 | 0.0376 |
| 19 | 0.1377 | 0.1161 | 0.0981 | 0.0829 | 0.0703 | 0.0596 | 0.0506 | 0.0431 | 0.0367 | 0.0313 |
| 20 | 0.1240 | 0.1037 | 0.0868 | 0.0728 | 0.0611 | 0.0514 | 0.0433 | 0.0365 | 0.0308 | 0.0261 |
| 25 | 0.0736 | 0.0588 | 0.0471 | 0.0378 | 0.0304 | 0.0245 | 0.0197 | 0.0160 | 0.0129 | 0.0105 |
| 30 | 0.0437 | 0.0334 | 0.0256 | 0.0196 | 0.0151 | 0.0116 | 0.090 | 0.0070 | 0.0054 | 0.0042 |
| 35 | 0.0259 | 0.0189 | 0.0139 | 0.0102 | 0.0075 | 0.0055 | 0.0041 | 0.0030 | 0.0023 | 0.0017 |
| 40 | 0.0154 | 0.0107 | 0.0075 | 0.0053 | 0.0037 | 0.0026 | 0.0019 | 0.0013 | 0.0010 | 0.0007 |
| 45 | 0.0091 | 0.0061 | 0.0041 | 0.0027 | 0.0019 | 0.0013 | 0.0009 | 0.0006 | 0.0004 | 0.0003 |
| 50 | 0.0054 | 0.0035 | 0.0022 | 0.0014 | 0.0009 | |||||
| Годы (n) | Процентные ставки (r) | |||||||||
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| 1 | 0.8264 | 0.8197 | 0.8130 | 0.8065 | 0.8000 | 0.7937 | 0.7874 | 0.7812 | 0.7752 | 0.7692 |
| 2 | 0.6830 | 0.6719 | 0.6610 | 0.6504 | 0.6400 | 0.6299 | 0.6200 | 0.6104 | 0.6009 | 0.5917 |
| 3 | 0.5645 | 0.5507 | 0.5374 | 0.5245 | 0.5120 | 0.4999 | 0.4882 | 0.4768 | 0.4658 | 0.4552 |
| 4 | 0.4665 | 0.4514 | 0.4369 | 0.4230 | 0.4096 | 0.3968 | 0.3844 | 0.3725 | 0.3611 | 0.3501 |
| 5 | 0.3855 | 0.3700 | 0.3552 | 0.3411 | 0.3277 | 0.3149 | 0.3027 | 0.2910 | 0.2799 | 0.2693 |
| 6 | 0.3186 | 0.3033 | 0.2888 | 0.2751 | 0.2621 | 0.2499 | 0.2383 | 0.2274 | 0.2170 | 0.2072 |
| 7 | 0.2633 | 0.2486 | 0.2348 | 0.2218 | 0.2097 | 0.1983 | 0.1877 | 0.1776 | 0.1682 | 0.1594 |
| 8 | 0.2176 | 0.2038 | 0.1909 | 0.1789 | 0.1678 | 0.1574 | 0.1478 | 0.1388 | 0.1304 | 0.1226 |
| 9 | 0.1799 | 0.1670 | 0.1552 | 0.1443 | 0.1342 | 0.1249 | 0.1164 | 0.1084 | 0.1011 | 0.0943 |
| 10 | 0.1486 | 0.1369 | 0.1262 | 0.1164 | 0.1074 | 0.0992 | 0.0916 | 0.0847 | 0.0784 | 0.0725 |
| 11 | 0.1228 | 0.1122 | 0.1026 | 0.0938 | 0.0859 | 0.0787 | 0.0721 | 0.0662 | 0.0607 | 0.0558 |
| 12 | 0.1015 | 0.0920 | 0.0834 | 0.0757 | 0.0687 | 0.0625 | 0.0568 | 0.0517 | 0.0471 | 0.0429 |
| 13 | 0.0839 | 0.0754 | 0.0678 | 0.0610 | 0.0550 | 0.0496 | 0.0447 | 0.0404 | 0.0365 | 0.0330 |
| 14 | 0.0693 | 0.0618 | 0.0551 | 0.0492 | 0.0440 | 0.0393 | 0.0352 | 0.0316 | 0.0283 | 0.0254 |
| 15 | 0.0573 | 0.0507 | 0.0448 | 0.0397 | 0.0352 | 0.0312 | 0.0277 | 0.0247 | 0.0219 | 0.0195 |
| 16 | 0.0474 | 0.0415 | 0.0364 | 0.0320 | 0.0281 | 0.0248 | 0.0218 | 0.0193 | 0.0170 | 0.0150 |
| 17 | 0.0391 | 0.0340 | 0.0296 | 0.0258 | 0.0225 | 0.0197 | 0.0172 | 0.0150 | 0.0132 | 0.0116 |
| 18 | 0.0323 | 0.0279 | 0.0241 | 0.0208 | 0.0180 | 0.0156 | 0.0135 | 0.0118 | 0.0102 | 0.0089 |
| 19 | 0.0267 | 0.0229 | 0.0196 | 0.0168 | 0.0144 | 0.0124 | 0.0107 | 0.0092 | 0.0079 | 0.0069 |
| 20 | 0.0221 | 0.0187 | 0.0159 | 0.0135 | 0.0115 | 0.0098 | 0.0084 | 0.0072 | 0.0061 | 0.0053 |
| 25 | 0.0085 | 0.0069 | 0.0057 | 0.0046 | 0.0038 | 0.0031 | 0.0025 | 0.0021 | 0.0017 | 0.0014 |
| 30 | 0.0033 | 0.0026 | 0.0020 | 0.0016 | 0.0012 | 0.0010 | 0.0008 | 0.0006 | 0.0005 | 0.0004 |
| 35 | 0.0013 | 0.0009 | 0.0007 | 0.0005 | 0.0004 | 0.0003 | 0.0002 | 0.0002 | 0.0001 | 0.0001 |
| 40 | 0.0005 | 0.0004 | 0.0003 | 0.0002 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0000 | 0.0000 |
| 45 | 0.0002 | 0.0001 | 0.0001 | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
Таблица 37.10 | 1 - (1 + r) -n |
Текущая стоимость аннуитета 1: | ----------------- |
r |
| Годы (n) | Процентные ставки (r) | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0.9901 | 0.9804 | 0.9709 | 0.9615 | 0.9524 | 0.9434 | 0.9346 | 0.9259 | 0.9174 | 0.9091 |
| 2 | 1.9704 | 1.9416 | 1.9135 | 1.8861 | 1.8594 | 1.8334 | 1.8080 | 1.7833 | 1.7591 | 1.7355 |
| 3 | 2.9410 | 2.8839 | 2.8286 | 2.7751 | 2.7232 | 2.6730 | 2.6243 | 2.5771 | 2.5313 | 2.4869 |
| 4 | 3.9020 | 3.8077 | 3.7171 | 3.6299 | 3.5460 | 3.4651 | 3.3872 | 3.3121 | 3.2397 | 3.1699 |
| 5 | 4.8534 | 4.7135 | 4.5797 | 4.4518 | 4.3295 | 4.2124 | 4.1002 | 3.9927 | 3.8897 | 3.7908 |
| 6 | 5.7955 | 5.6014 | 5.4172 | 5.2421 | 5.0757 | 4.9173 | 4.7665 | 4.6229 | 4.4859 | 4.3553 |
| 7 | 6.7282 | 6.4720 | 6.2303 | 6.0021 | 5.7864 | 5.5824 | 5.3893 | 5.2064 | 5.0330 | 4.8684 |
| 8 | 7.6517 | 7.3255 | 7.0197 | 6.7327 | 6.4632 | 6.2098 | 5.9713 | 5.7466 | 5.5348 | 5.3349 |
| 9 | 8.5660 | 8.1622 | 7.7861 | 7.4353 | 7.1078 | 6.8017 | 6.5152 | 6.2469 | 5.9952 | 5.7590 |
| 10 | 9.4713 | 8.9826 | 8.5302 | 8.1109 | 7.7217 | 7.3601 | 7.0236 | 6.7101 | 6.4177 | 6.1446 |
| 11 | 10.3676 | 9.7868 | 9.2526 | 8.7605 | 8.3064 | 7.8869 | 7.4987 | 7.1390 | 6.8052 | 6.4951 |
| 12 | 11.2551 | 10.5753 | 9.9540 | 9.3851 | 8.8633 | 8.3838 | 7.9427 | 7.5361 | 7.1607 | 6.8137 |
| 13 | 12.1337 | 11.3484 | 10.6350 | 9.9856 | 9.3936 | 8.8527 | 8.3577 | 7.9038 | 7.4869 | 7.1034 |
| 14 | 13.0037 | 12.1062 | 11.2961 | 10.5631 | 9.8986 | 9.2950 | 8.7455 | 8.2442 | 7.7862 | 7.3667 |
| 15 | 13.8651 | 12.8493 | 11.9379 | 11.1184 | 10.3797 | 9.7122 | 9.1079 | 8.5595 | 8.0607 | 7.6061 |
| 16 | 14.7179 | 13.5777 | 12.5611 | 11.6523 | 10.8378 | 10.1059 | 9.4466 | 8.8514 | 8.3126 | 7.8237 |
| 17 | 15.5623 | 14.2919 | 13.1661 | 12.1657 | 11.2741 | 10.4773 | 9.7632 | 9.1216 | 8.5436 | 8.0216 |
| 18 | 16.3983 | 14.9920 | 13.7535 | 12.6593 | 11.6896 | 10.8276 | 10.0591 | 9.3719 | 8.7556 | 8.2014 |
| 19 | 17.2260 | 15.6785 | 14.3238 | 13.1339 | 12.0863 | 11.1581 | 10.3356 | 9.6036 | 8.9501 | 8.3649 |
| 20 | 18.0456 | 16.3514 | 14.8775 | 13.5903 | 12.4622 | 11.4699 | 10.5940 | 9.8181 | 9.1285 | 8.5136 |
| 25 | 22.0232 | 19.5235 | 17.4131 | 15.6221 | 14.0939 | 12.7834 | 11.6536 | 10.6748 | 9.8226 | 9.0770 |
| 30 | 25.8077 | 22.3965 | 19.6004 | 17.2920 | 15.3725 | 13.7648 | 12.4090 | 11.2578 | 10.2737 | 9.4269 |
| 35 | 29.4086 | 24.9986 | 21.4872 | 18.6646 | 16.3742 | 14.4982 | 12.9477 | 11.6546 | 10.5668 | 9.6442 |
| 40 | 32.8347 | 27.3555 | 23.1148 | 19.7928 | 17.1591 | 15.0463 | 13.3317 | 11.9246 | 10.7574 | 9.7791 |
| 45 | 36.0945 | 29.4902 | 24.5187 | 20.7200 | 17.7741 | 15.4558 | 13.6055 | 12.1084 | 10.8812 | 9.8628 |
| 50 | 39.1961 | 31.4236 | 25.7298 | 21.4822 | 18.2559 | 15.7619 | 13.8007 | 12.2335 | 10.9617 | 9.9148 |
| Годы (n) | Процентные ставки (r) | |||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 1 | 0.9009 | 0.8929 | 0.8850 | 0.8772 | 0.8696 | 0.8621 | 0.8547 | 0.8475 | 0.8403 | 0.8333 |
| 2 | 1.7125 | 1.6901 | 1.6681 | 1.6467 | 1.6257 | 1.6052 | 1.5852 | 1.5656 | 1.5465 | 1.5278 |
| 3 | 2.4437 | 2.4018 | 2.3612 | 2.3216 | 2.2832 | 2.2459 | 2.2096 | 2.1743 | 2.1399 | 2.1065 |
| 4 | 3.1024 | 3.0373 | 2.9745 | 2.9137 | 2.8550 | 2.7982 | 2.7432 | 2.6901 | 2.6386 | 2.5887 |
| 5 | 3.6959 | 3.6048 | 3.5172 | 3.4331 | 3.3522 | 3.2743 | 3.1993 | 3.1272 | 3.0576 | 2.9906 |
| 6 | 4.2305 | 4.1114 | 3.9975 | 3.8887 | 3.7845 | 3.6847 | 3.5892 | 3.4976 | 3.4098 | 3.3255 |
| 7 | 4.7122 | 4.5638 | 4.4226 | 4.2883 | 4.1604 | 4.0386 | 3.9224 | 3.8115 | 3.7057 | 3.6046 |
| 8 | 5.1461 | 4.9676 | 4.7988 | 4.6389 | 4.4873 | 4.3436 | 4.2072 | 4.0776 | 3.9544 | 3.8372 |
| 9 | 5.5370 | 5.3282 | 5.1317 | 4.9464 | 4.7716 | 4.6065 | 4.4506 | 4.3030 | 4.1633 | 4.0310 |
| 10 | 5.8892 | 5.6502 | 5.4262 | 5.2161 | 5.0188 | 4.8332 | 4.6586 | 4.4941 | 4.3389 | 4.1925 |
| 11 | 6.2065 | 5.9377 | 5.6869 | 5.4527 | 5.2337 | 5.0286 | 4.8364 | 4.6560 | 4.4865 | 4.3271 |
| 12 | 6.4924 | 6.1944 | 5.9176 | 5.6603 | 5.4206 | 5.1971 | 4.9884 | 4.7932 | 4.6105 | 4.4392 |
| 13 | 6.7499 | 6.4235 | 6.1218 | 5.8424 | 5.5831 | 5.3423 | 5.1183 | 4.9095 | 4.7147 | 4.5327 |
| 14 | 6.9819 | 6.6282 | 6.3025 | 6.0021 | 5.7244 | 5.4675 | 5.2293 | 5.0081 | 4.8023 | 4.6106 |
| 15 | 7.1909 | 6.8109 | 6.4624 | 6.1422 | 5.8473 | 5.5755 | 5.3242 | 5.0916 | 4.8759 | 4.6755 |
| 16 | 7.3792 | 6.9740 | 6.6039 | 6.2651 | 5.9542 | 5.6685 | 5.4053 | 5.1624 | 4.9377 | 4.7296 |
| 17 | 7.5488 | 7.1196 | 6.7291 | 6.3729 | 6.0471 | 5.7487 | 5.4746 | 5.2223 | 4.9897 | 4.7746 |
| 18 | 7.7016 | 7.2497 | 6.8399 | 6.4675 | 6.1279 | 5.8178 | 5.5339 | 5.2732 | 5.0333 | 4.8122 |
| 19 | 7.8393 | 7.3658 | 6.9380 | 6.5504 | 6.1982 | 5.8775 | 5.5845 | 5.3162 | 5.0700 | 4.8435 |
| 20 | 7.9633 | 7.4694 | 7.0248 | 6.6231 | 6.2593 | 5.9288 | 5.6278 | 5.3527 | 5.1009 | 4.8696 |
| 25 | 8.4217 | 7.8431 | 7.3300 | 6.8729 | 6.4641 | 6.0971 | 5.7662 | 5.4669 | 5.1951 | 4.9476 |
| 30 | 8.6938 | 8.0552 | 7.4957 | 7.0027 | 6.5660 | 6.1772 | 5.8294 | 5.5168 | 5.2347 | 4.9789 |
| 35 | 8.8552 | 8.1755 | 7.5856 | 7.0700 | 6.6166 | 6.2153 | 5.8582 | 5.5386 | 5.2512 | 4.9915 |
| 40 | 8.9511 | 8.2438 | 7.6344 | 7.1050 | 6.6418 | 6.2335 | 5.8713 | 5.5482 | 5.2582 | 4.9966 |
| 45 | 9.0079 | 8.2825 | 7.6609 | 7.1232 | 6.6542 | 6.2421 | 5.8773 | 5.5523 | 5.2611 | 4.9986 |
| 50 | 9.0417 | 8.3045 | 7.6752 | 7.1327 | 6.6603 | 6.2463 | 5.8801 | 5.5541 | 5.2623 | 4.9995 |
| Годы (n) | Процентные ставки (r) | |||||||||
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| 1 | 0.8264 | 0.8197 | 0.8130 | 0.8065 | 0.8000 | 0.7937 | 0.7874 | 0.7812 | 0.7752 | 0.7692 |
| 2 | 1.5095 | 1.4915 | 1.4740 | 1.4568 | 1.4400 | 1.4235 | 1.4074 | 1.3916 | 1.3761 | 1.3609 |
| 3 | 2.0739 | 2.0422 | 2.0114 | 4.9813 | 1.9520 | 1.9234 | 1.8956 | 1.8684 | 1.8420 | 1.8161 |
| 4 | 2.5404 | 2.4936 | 2.4483 | 2.4043 | 2.3616 | 2.3202 | 2.2800 | 2.2410 | 2.2031 | 2.1662 |
| 5 | 2.9260 | 2.8636 | 2.8035 | 2.7454 | 2.6893 | 2.6351 | 2.5827 | 2.5320 | 2.4830 | 2.4356 |
| 6 | 3.2446 | 3.1669 | 3.0923 | 3.0205 | 2.9514 | 2.8850 | 2.8210 | 2.7594 | 2.7000 | 2.6427 |
| 7 | 3.5079 | 3.4155 | 3.3270 | 3.2423 | 3.1611 | 3.0833 | 3.0087 | 2.9370 | 2.8682 | 2.8021 |
| 8 | 3.7256 | 3.6193 | 3.5179 | 3.4212 | 3.3289 | 3.2407 | 3.1564 | 3.0758 | 2.9986 | 2.9247 |
| 9 | 3.9054 | 3.7863 | 3.6731 | 3.5655 | 3.4631 | 3.3657 | 3.2728 | 3.1842 | 3.0997 | 3.0190 |
| 10 | 4.0541 | 3.9232 | 3.7993 | 3.6819 | 3.5705 | 3.4648 | 3.3644 | 3.2689 | 3.1781 | 3.0915 |
| 11 | 4.1769 | 4.0354 | 3.9018 | 3.7757 | 3.6564 | 3.5435 | 3.4365 | 3.3351 | 3.2388 | 3.1473 |
| 12 | 4.2784 | 4.1274 | 3.9852 | 3.8514 | 3.7251 | 3.6059 | 3.4933 | 3.3868 | 3.2859 | 3.1903 |
| 13 | 4.3624 | 4.2028 | 4.0530 | 3.9124 | 3.7801 | 3.6555 | 3.5381 | 3.4272 | 3.3224 | 3.2233 |
| 14 | 4.4317 | 4.2646 | 4.1082 | 3.9616 | 3.8241 | 3.6949 | 3.5733 | 3.4587 | 3.3507 | 3.2487 |
| 15 | 4.4890 | 4.3152 | 4.1530 | 4.0013 | 3.8593 | 3.7261 | 3.6010 | 3.4834 | 3.3726 | 3.2682 |
| 16 | 4.5364 | 4.3567 | 4.1894 | 4.0333 | 3.8874 | 3.7509 | 3.6228 | 3.5026 | 3.3896 | 3.2832 |
| 17 | 4.5755 | 4.3908 | 4.2190 | 4.0591 | 3.9099 | 3.7705 | 3.6400 | 3.5177 | 3.4028 | 3.2948 |
| 18 | 4.6079 | 4.4187 | 4.2431 | 4.0799 | 3.9279 | 3.7861 | 3.6536 | 3.5294 | 3.4130 | 3.3037 |
| 19 | 4.6346 | 4.4415 | 4.2627 | 4.0967 | 3.9424 | 3.7985 | 3.6642 | 3.5386 | 3.4210 | 3.3105 |
| 20 | 4.6567 | 4.4603 | 4.2786 | 4.1103 | 3.9539 | 3.8083 | 3.6726 | 3.5458 | 3.4271 | 3.3158 |
| 25 | 4.7213 | 4.5139 | 4.3232 | 4.1474 | 3.9849 | 3.8342 | 3.6943 | 3.5640 | 3.4423 | 3.3286 |
| 30 | 4.7463 | 4.5338 | 4.3391 | 4.1601 | 3.9950 | 3.8424 | 3.7009 | 3.5693 | 3.4466 | 3.3321 |
| 35 | 4.7559 | 4.5411 | 4.3447 | 4.1644 | 3.9984 | 3.8450 | 3.7028 | 3.5708 | 3.4478 | 3.3330 |
| 40 | 4.7596 | 4.5439 | 4.3467 | 4.1659 | 3.9995 | 3.8458 | 3.7034 | 3.5712 | 3.4481 | 3.3332 |
| 45 | 4.7610 | 4.5449 | 4.3474 | 4.1664 | 3.9998 | 3.8460 | 3.7036 | 3.5714 | 3.4482 | 3.3333 |
| 50 | 4.7616 | 4.5452 | 4.3477 | 4.1666 | 3.9999 | 3.8461 | 3.7037 | 3.5714 | 3.4483 | 3.3333 |
Ответы на контрольное задание
Вы должны рассчитать NPV проекта на основе различных периодов удержания. Это показывается следующим образом:
| Год | NCF | Стоимость лома | Коэффи- циент дисконти- рования 18% | PV годовых прибылей | PV стои- мости лома | NPV накоп. сумма |
| $ | $ | $ | $ | $ | $ | |
| 0 | (25,000) | 1.000 | (25,000) | |||
| 1 | 4,000 | 22,500 | 0.848 | 3,392 | 19,080 | (2,528) |
| 2 | 6,000 | 18,000 | 0.718 | 4,308 | 12,924 | (4,376) |
| 3 | 10,000 | 16,000 | 0.609 | 6,090 | 9,744 | (1,466) |
| 4 | 10,000 | 15,000 | 0.516 | 5,160 | 7,740 | 1,690 |
| 5 | 10,000 | 12,500 | 0.437 | 4,370 | 5,462 | 3,782 |
| 6 | 10,000 | 0 | 3,700 | 0 | 2,020 |
Каждая цифра в колонке накопленной суммы равняется сумме PV затрат и прибылей к дате плюс PV стоимости лома текущего периода. Из этой таблицы очевидно, что прекращение проекта в течение первых трех лет могло бы привести к отрицательному значению NPV. Вы должны порекомендовать управлению вложить средства в проект, но не прерывать его в течение пяти лет (наивысшее значение NPV). Вам также следует посоветовать им отслеживать ситуацию и проверять расчеты и прогнозы по мере необходимости, поскольку все цифры, на которых базируется ваша рекомендация, являются прогнозируемыми показателями.

