О поиске решения для задачи подбора исторического курса при переводе финансовой отчетности в иностранной валюте
Андрей Гершун
Начало в выпусках: #47, #49, #50
Часть 5
Насколько точны приблизительные способы расчета исторического курса?Естественно, перед тем, как использовать тот или иной приблизительный способ расчета исторического курса, задаться вопросом: а насколько точен этот способ? Для проверки точности различных способов давайте проведем ряд экспериментов.
Средний курсДля проверки точности метода среднего курса мы промоделируем движение денег по счету за определенный период. В качестве исходной таблицы курсов 
мы возьмем колебания курса за 1998 год и начало 1999 года. Проводки по счету 
мы будем моделировать случайной функцией, которая для каждого дня будет нам выдавать значение в интревале от 0 до 1.
Программа тестирования будет работать по следующему алгоритму. Для каждого месяца из 1998 года выполняется достаточно большое количество тестов (в нашем эксперименте мы выбирем их число 
равным 100,000, дальнейшее увеличение количества испытаний практически не дает улучшения оценок) и выполним следующие действия:
а) Создается массив проводок (на каждую дату сумма проводки может принимать случайное значение от 0 до 1);
б) Рассчитывается сумма оборота в рублях 
;
в) Рассчитывается точное значение оборота в долларах 
. Полученное значение будем считать эталонным;
г) Рассчитывается средний курс по формуле 
;
д) Эталонное значение 
сравнивается с приблизительным значением 
. Для каждого теста накапливается разница 
, которая обозначает относительную ошибку, полученную в данном тесте.
е) Данные об ошибках всех тестов суммируются, и мы рассчитываем стандартное отклонение (дисперсию) по формуле 
[2, стр.380].
Для чего мы рассчитали дисперсию? Основная причина заключается в неравенстве Чебышева [3, стр. 428], которое устанваливает важное свойство дисперсии:
.
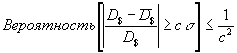На качественном уровне это значит, что значение 
будет редко принимать значения, далекие от 
если дисперсия 
мала, и в 75% случаев 
будет лежать в интервале 
, а в 99% случаев 
.
На основе данных тестовой программы получаем следующие значения для 12 месяцев 1998 года и первых 8 месяцев 1999 года:
Месяц |
|
|
| Январь 98 | 0.00004 | 0.0% |
| Февраль 98 | 0.00002 | 0.02% |
| Март 98 | 0.00001 | 0.01% |
| Апрель 98 | 0.00006 | 0.06% |
| Май 98 | 0.00003 | 0.03% |
| Июнь 98 | 0.00002 | 0.02% |
| Июль 98 | 0.00004 | 0.04% |
| Август 98 | 0.00311 | 3.11% |
| Сентябрь 98 | 0.00666 | 6.66% |
| Октябрь 98 | 0.00024 | 0.24% |
| Ноябрь 98 | 0.00098 | 0.98% |
| Декабрь 98 | 0.00105 | 1.05% |
| Январь 99 | 0.00047 | 0.47% |
| Февраль 99 | 0.00017 | 0.17% |
| Март 99 | 0.00006 | 0.06% |
| Апрель 99 | 0.00047 | 0.47% |
| Май 99 | 0.00010 | 0.10% |
| Июнь 99 | 0.00004 | 0.04% |
| Июль 99 | 0.00009 | 0.09% |
| Август 99 | 0.00018 | 0.18% |
То есть в сентябре 1998 года применение среднего курса вместо точного расчета в 99% случаев (то есть практически при любых проводках в течение месяца) даст ошибку меньшую, чем 
. В другие месяцы ошибка будет еще меньше.
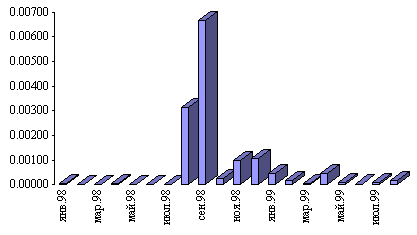
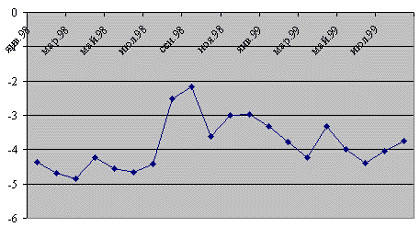
На приведенном графике изображено значение , а также для наглядности приведен график логарифма 
(то есть значение по вертикали определяет порядок ).
Кстати, для всего 1998 года целиком по результатам расчета 
, что означает высокую вероятность 
искажения при применении среднего курса.
А стоит ли применять средний курс?
Результаты другого эксперимента показывают, что использование средневзвешенного курса, которые может быть рассчитан по формуле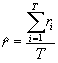 
дает значительно лучшие результаты. В приведенной ниже таблице указаны значения отклонения, рассчитанные для среднего и средневзвешенного курса.
Месяц |
|
| (1)/(2) |
| Январь 98 | 0.000034 | 0.000042 | 1.3 |
| Февраль 98 | 0.000020 | 0.000020 | 1.0 |
| Март 98 | 0.000014 | 0.000014 | 1.0 |
| Апрель 98 | 0.000011 | 0.000059 | 5.6 |
| Май 98 | 0.000015 | 0.000027 | 1.9 |
| Июнь 98 | 0.000015 | 0.000022 | 1.5 |
| Июль 98 | 0.000013 | 0.000039 | 3.0 |
| Август 98 | 0.000675 | 0.003111 | 4.6 |
| Сентябрь 98 | 0.000855 | 0.006675 | 7.8 |
| Октябрь 98 | 0.000195 | 0.000247 | 1.3 |
| Ноябрь 98 | 0.000184 | 0.000976 | 5.3 |
| Декабрь 98 | 0.000107 | 0.001054 | 9.9 |
| Январь 99 | 0.000087 | 0.000475 | 5.5 |
| Февраль 99 | 0.000014 | 0.000170 | 12.2 |
| Март 99 | 0.000047 | 0.000059 | 1.3 |
| Апрель 99 | 0.000023 | 0.000466 | 20.5 |
| Май 99 | 0.000027 | 0.000103 | 3.8 |
| Июнь 99 | 0.000006 | 0.000040 | 6.5 |
| Июль 99 | 0.000007 | 0.000091 | 12.4 |
| Август 99 | 0.000022 | 0.000182 | 8.3 |
Как видно, применение средневзвешенного курса дает улучшение оценки от 1.2 до 20 раз! То есть при незначительных дополнительных затратах времени можно получить значительно более точное значение 
.
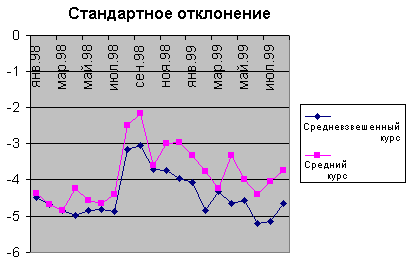
На графике приведены десятичные логарифмы отклонений для среднего и средневзвешенного курса для 1998 и начала 1999 года.
2. Siegel, Joe G. Dictionary of accounting terms, 2 ed., Barron Educational Series, Inc., New York, 1995
ISBN 0-8120-1918-0
3. Грэхем Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики: Пер. с англ. - М.: Мир, 1998.
ISBN 5-03-001793-3
Продолжение в следующем выпуске.
