Лимитирующие факторы и принятие решения
|
| Учебный курс АССА |
| Цели / Лимитирующие факторы и принятие решения | Ситуации, включающие один лимитирующий фактор | Ситуации, включающие более одного лимитирующего фактора | Контрольное задание | Ответы на контрольные задания |
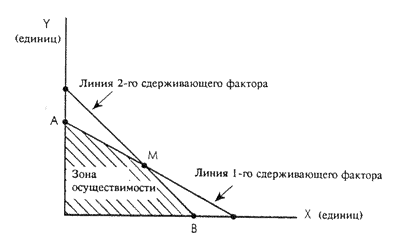
| Мы рассмотрели ситуацию, затрагивающую один лимитирующий фактор, но на практике Вы обнаружите, что большинство предприятий функционируют в условиях двух или более лимитирующих факторов. В тех случаях, когда на предприятие воздействуют более одного лимитирующих факторов и оно производит для продажи два или более видов продукции или услуг, руководство сталкивается с необходимостью решать, каким образом распределить ограниченные ресурсы на различные виды продукции или услуг так, чтобы максимально повысить результаты деятельности предприятия. Очевидно, что руководству пришлось бы решать более простую задачу, если бы компания производила для продажи только один вид продукции, поскольку в этом случае все ресурсы полностью распределялись бы на этот единственный продукт. Линейное программированиеЛинейное программирование является математическим методом, разработанным для помощи руководству в распределении ограниченных ресурсов предприятия, которое производит для реализации более одной единицы затрат и функционирует в условиях двух или более лимитирующих факторов. Графический подход к линейному программированию используется в тех ситуациях, когда компания производит только два вида продукции или услуг и действует в условиях двух или более лимитирующих факторов. Именно эта часть линейного программирования будет рассмотрена в данном блоке. Мы также ограничим наше изучение ситуациями, включающими не более двух лимитирующих факторов. Графический метод может применяться в ситуациях, когда речь идет о более чем двух лимитирующих факторах, но в этой рабочей тетради мы не будем рассматривать такие примеры. В ситуациях, когда предприятие производит более двух видов продукции или услуг и при этом является объектом воздействия многочисленных лимитирующих факторов, для помощи руководству в распределении ресурсов используется более передовой метод линейного программирования, названный симплексным методом. Вам будет приятно узнать, что симплексный метод не включен в программу этого курса, но Вы должны иметь представление о том, что такой метод существует.
Рисунок 17.1 Графический подход к линейному программированию При использовании графического подхода к линейному программированию необходимо придерживаться следующей процедуры:
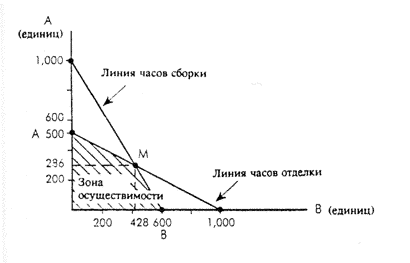
ЗаданиеКомпания Бест Лтд выпускает два вида продукции - А и В. В отношении этой компании и ее продукции имеется следующая информация:
Прямые затраты труда ограничены в цехах сборки и отделки до максимальной величины 3,000 часов и 2,000 часов, соответственно. Используя графический подход к линейному программированию, определите ассортимент продукции, который максимально увеличивает прибыль, получаемую Бест Лтд. Первое, что Вы могли заметить в этом задании, заключается в отсутствии упоминания о постоянных затратах. Постоянные затраты, по определению, не подвержены воздействию со стороны ассортимента продукции или уровня деловой активности предприятия и, следовательно, не имеют отношения к этому решению (т.е. постоянные затраты останутся неизменными независимо от действий руководства). Постоянные затраты будут относиться к этому решению только в том случае, если они будут подвергаться определенному воздействию за счет изменения в ассортименте продукции. Перед тем как начать построение графика, вам необходимо определить две точки на каждой из линий лимитирующего фактора следующим образом: Фактор затрат на сборку
Фактор затрат на отделку
Теперь мы можем построить наш график:
Проверим три оптимально возможных сочетания: Точка A: где A = 500 изделий и B = 0 изделий Маржинальный доход = $5,000 Точка M: где A = 286 изделий и B = 428 изделий (в экзаменационном задании от вас потребуется только определить при помощи графика соответствующее количество изделий до ближайшего десятка или сотни и т.д.) Маржинальный доход = (286 х $10) + (428 х $8) = $6,284 Точка B: где A = 0 изделий и B = 600 изделий Маржинальный доход = $4,800 Таким образом, ассортимент продукции, который максимально увеличивает прибыль Бест Лтд, находится в точке M (т.е. 286 изделий A и 428 изделий B) и создает маржинальный доход для компании в размере $6,284, за счет которого покрываются постоянные затраты и обеспечивается остаток, представляющий прибыль, получаемую компанией. |
| <<предыдущая | [1][2][3][4][5] | следующая>> |
| [вид для печати] | ||
| © ЗАО "Аскери-АССА" | ||