Дисконтированное движение денежных средств (DCF)

Как правило, оба эти метода приводят к одинаковым решениям на "принятие" или "отклонение". Но есть обстоятельства, в которых они могут дать противоположные результаты:

• когда проекты имеют противоположные фазы потока денежных средств;
• когда проекты имеют разные по размерам затраты;
• когда проекты различаются по продолжительности во времени;
• когда имеются нерегулярные потоки денежных средств, вызывающие на протяжении периода реализации проекта череду доходов и расходов, приводящие к многочисленным IRR.

Чтобы проиллюстрировать это, мы снова рассмотрим проекты А и В, но изменим поток денежных средств для проекта В. Теперь они выглядят так, как показано в таблице 37.4.

Теперь Проект А лишь незначительно привлекательнее, чем проект В. Это связано с тем, что больше средств денежного потока возникает на более раннем этапе реализации проекта, и предполагается, что прибыли реинвестируются с IRR. Однако это не всегда может быть так, поскольку возможности инвестировать эти средства с таким уровнем доходности могут отсутствовать.

Допуская, что ставка дисконта будет равняться требуемой норме прибыли, какой проект Вы бы выбрали при 12%? Рассчитайте текущую стоимость для обоих проектов при 12%.

Таблица 37.5 показывает предпосылки изменений распределения во времени потоков денежных средств для ставки дисконта 12%. Конечно же показатели для проекта А остаются такими же, как и раньше (рисунок 37.1), поскольку его поток денежных средств не изменился. (Коэффициенты берутся из таблицы 37.9).

Здесь возникает дилемма, потому что NPV абсолютно одинакова в обоих случаях. В идеальном мире определенности вам безразлично, какой проект выбирать, А или В, потому что NPV одинакова. Так какой же следует выбрать? Проект А имеет более высокий уровень доходности IRR, и по этой причине выбрать следует его. Это может оказаться правильным, но было бы неверно допускать, что проект с наивысшей IRR обязательно следует выбирать. В таблице 37.6 вновь рассматриваются проекты А и В при ставке дисконта 10%.

Это создает дополнительную проблему, потому что проект В теперь показывает более высокую NPV, чем проект А. Возникает прямое противоречие между выбором, предложенным по методу NPV, проект В, и выбором, предложенным по методу IRR, проект А.

Схема, показанная в таблице 37.7, обобщает NPV проектов А и В для диапазона ставок дисконта и варианты выбора, на которые указывают методы NPV и IRR.

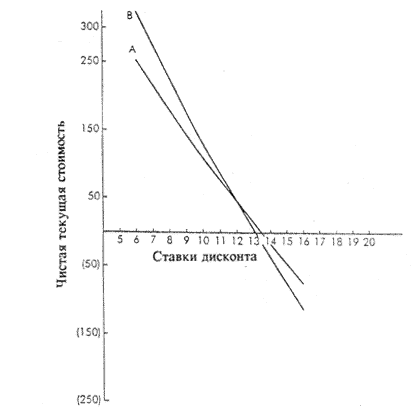
Их также можно представить графически, как показано на Рисунке 37.2.

Рисунок 37.2 Чистая текущая стоимость в диапазоне ставок дисконта

Значения NPV располагаются по вертикальной оси, а ставки дисконта - по горизонтальной. Две линии А и В пересекаются на значении ставки дисконта в 12% и NPV - 46, и каждая пересекает горизонтальную ось в точке, соответствующей ее значению IRR, т.е. 13.5 для А и 13.1 для В. По методу NPV, когда ставка дисконта падает ниже 12%, проект В становится более привлекательным. Когда она превышает 12%, более привлекательным оказывается А.